Level Set Toolbox
(precompiled mex files for Mac and 64-bit Linux, source code for other platforms)
To install, download the toolbox, unzip it to the desired location, and add that location to your MATLAB path. To get started, try running Example_2D.m in the DensitySingle, RegressionSingle, and RegressionMulti directories to perform single density level set estimation, single regression level set estimation, and multiple simultaneous level set esetimation, respectively. This toolbox contains C mex files to be used with MATLAB. The methods require O(N log N) computations.

Regression level set estimation example:

In general, a level set S is the set on which f exceeds some critical value (e.g. S = {x : f(x) > γ}). An example two-dimensional function f, a digital elevation map of St. Louis, is in Figure a, and one of its level sets is displayed in Figure b. Boundaries of such sets typically constitute submanifolds embedded in the high-dimensional observation space. Extracting a level set estimate by simply thresholding noisy observations (such as those displayed in Figure c) results in a highly inaccurate result which does not exploit the submanifold structure of the true level set; this is indicated by the result in Figure d. Because set identification is intrinsically simpler than function denoising or estimation, explicit set extraction methods can achieve higher accuracy than more indirect approaches. For example, extracting the set of interest from a denoised version of the observations results in an oversmoothed estimate of the target submanifold, as displayed in Figure e. We have developed a set estimation framework which automatically adapts to the spatially varying regularity of both the boundary of the level set and the function underlying the data, resulting in highly accurate estimates such as the one displayed in Figure f.

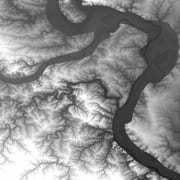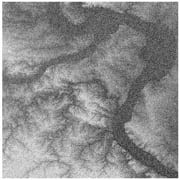(a)	(b)	(c)
(d)	(e)	(f)

Our framework constitutes a significant paradigm shift from conventional set estimation methods based on complex Bayesian priors or active contour models. It was developed by deriving a computationally tractable error minimization criterion based on fundamental statistical principles. This novel objective function shares several desirable properties with objectives used by snakes and active contours, yet admits a thorough statistical analysis and bypasses complicated parameter tuning issues. In additional to showing compelling empirical support for this approach, we have demonstrated that it results in an estimator which exhibits near-minimax optimal rates of error convergence. This work has immediate application to problems such as detecting active brain regions from fMRI data and rapidly extracting critical level sets from digital terrain elevation data (DTED) for robust UAV navigation.